こんにちは!しまりす学園のぽんずです!
大学2年生の時にTOEICを本格的に勉強し始めて在学中に910点を取ることができ、現在は英語が苦手な方に向けて様々な情報を発信しています!
また、家庭教師を通じて基礎レベルの数学を教えていたので、数学が苦手な方に向けて数学の情報も発信しています!

今回は因数分解について解説していくよ

展開はできるけど、因数分解になると訳がわからなくなります
因数分解。
中学3年生の時に習うであろう単元ですが、ここで苦戦する方も珍しくありません。
いかんせんパターンが豊富で使いこなすのが大変なんですよね。
ですが!
なんと因数分解は共通因数とバッテン方式の2つさえ覚えてくれれば大丈夫なんです!
複雑だから数学は難しく感じる、シンプルにすればなんてことないんです。
因数分解を攻略する前に、展開と因数分解は表裏一体なので、まずは展開を理解してから因数分解に挑戦しましょう。
こちらの投稿を読んでくだされば展開については理解できます!
今日を機に因数分解のに対する苦手意識とおさらばしましょう!
ではよろしくお願いします!
因数分解とは

そもそも因数分解ってどういう意味なんですか?
あれ何をしているのかさっぱりわかりません

因数分解っていうのは一言でいうと、ある数や式を掛け算に変形することなんだ
「ある数や式を掛け算に変形すること」と言われてもピンとこないと思います。
この意味を理解するためには、まず因数という言葉を理解しないといけないですよね。
因数というのは、数や式を掛け算の形にしたときに掛け合わされている一つ一つの数や式のことです。
簡単な例で言うと、15を掛け算の形にすると3×5になりますよね。
この3と5が因数と呼ばれるんです。
つまり因数分解は因数を分解すると言うことなので、
15=3×5というこの形がある意味因数分解になるんですね。
なぜなら15を3と5という因数に分解することができているからです。
そして、15という数が3×5という掛け算の形に変形されていますね。
これで「ある数や式を掛け算に変形すること」という説明が理解できたと思います!
因数分解とはある数や式を掛け算に変形することである
因数分解と展開の関係性

そういえば、なんで展開を勉強してから因数分解を勉強するんですか?

因数分解は展開の逆バージョンだからだよ
左から右が展開、右から左が因数分解
そうなんです。
因数分解は展開の逆。たったこれだけなんです。
上の数式を見てください。
右から左の操作が因数分解なんですが、しっかりx+2とx+5の掛け算になってますね。
そしてもちろん左から右の操作は展開。
なので、展開をまず理解して、その上で展開でやったことの逆をしてあげる。
これで因数分解はマスターできるんですね。

因数分解は展開の逆なんですね!
でもどうやったら右の状態から左の式にできるんだろう?

それをこれから説明していくよ
因数分解のやり方
覚えることは2つだけでいい

おそらく因数分解の方法は5つあると言われているよ

こんなにもあるんですね、やる気がなくなります。

ただ安心して欲しいよ。
こんなに覚える必要はなくて、たった2つだけ覚えてくれればいいんだ。
因数分解で覚えるべきはたった2つ!
これは数学嫌いの方には朗報なのではないでしょうか?
で、じゃあ何を覚えればいいのかという話だと思います。
それは、共通因数とバッテン方式です!
そいつらなんですかい?と思った方、次で説明するのでご安心ください。
共通因数
共通因数というのは上の表の一番上のことを言います。
因数というのはさっきも話したように、掛け算で表した時の文字や数字たちのことです。
その因数が共通しているというのが共通因数という言葉の意味なんですね。
上の表のやつは文字ばっかりなのでもう少しわかりやすい例を使って説明します。
上の式は共通因数で因数分解した例です。
どうやったかというとまずは5xと10を掛け算の形にそれぞれ直してみます。
5xは5とxの掛け算、10は2と5の掛け算の形に直せます。
そしてこの5,x,2,5はそれぞれ因数とも呼べますね。
ここで注目して欲しいのが、5xと10どちらも5という共通した因数を持っていませんか?
そう、今回ではこの5を共通因数と呼ぶんです!
なのであとはその5を抽出して、計算したら5x+10になるようにしてあげる。
やり方は余り物のxと2を足し算で繋げて( )で閉じてしまえばいいのです。
共通の因数を見つけ出して、余りものを足し算で繋げて( )で閉じる。
これで共通因数はクリアです!
そして因数分解はまず、この共通因数があるかどうかを確認することから始まるので覚えておいてください。
バッテン方式
バッテン方式って何?と思った方が100%な気がします。
なぜなら私が命名したからです。
実を言うと高校数学で襷掛けと呼ばれる手法と丸かぶりしているのですが、親しみやすいようにバッテン方式と命名しました。
バッテン方式はすごく自分が高校生の時に思っていたよりも万能で、なんと表の下4つの式をバッテン方式一つでクリアすることができるんです!
改めてですが、バッテン方式を理解するためにこの展開を理解しておいてください。
ではまず細かいメカニズムを話す前にバッテン方式のやり方を説明していきます。
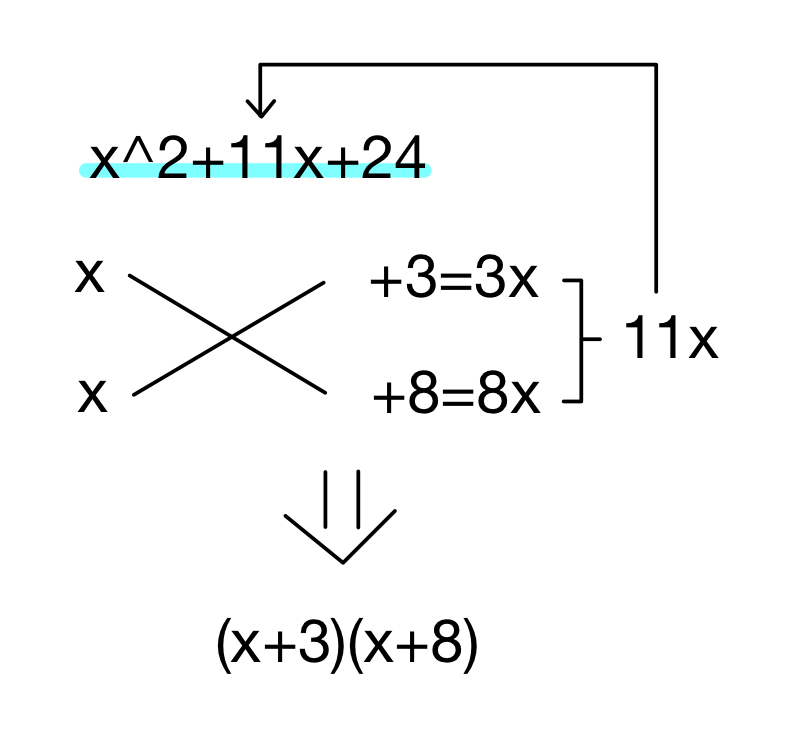
水色のラインが引かれている式が問題です。これを因数分解してみます。
※x^2はxの2乗という意味
まずは左端と右端の数字や文字に注目します。
そして何かをかけた結果その文字や数字になるものを書きます。
今回で言うと、右端のx^2はxとxをかけて、左端の24は+3と+8をかけると24になるので下にそう書きます。
(左端の3と8に+を書いた理由は後わかります。)
次にその書いた数字たちをバッテンで結び、掛け算します。
ここでバッテンをするからバッテン方式と命名しましたし、襷掛けと世間では呼ばれているんですね。
実際にバッテンで掛け算すると3xと8xになりました。
その次はこの3xと8xを足してみます。
そうすると11xになります。
これが最初の問題の真ん中の数字と一致すれば成功です!
今回は実際に一致しているので成功していて、最後のステップに進めます。
最後は最初に書いたバッテンのところにただ( )を付け加えるだけです。
そうすればあら不思議。答えになっているのではありませんか!
ちなみに左端の3と8に+を書いたのは( )をただつけるだけだと、(x 3)(x 8)と変な見た目になってしまうからでした。

バッテン方式。いいやり方だけど、なんでこれで因数分解が成立するの?

理由は展開の逆を横ではなく縦に考えているだけだからなんだ。
さぁ今の一言で理解できる方がいるのでしょうか?
いやいません、こんな変な文章わかるはずがないです。
ですが、ちゃんとわかるようになります!
これからバッテン方式が成立する論理を説明するんですが、めんどくさい方は読まなくても大丈夫です。
極論問題が解ければテストで点が取れるので最悪ロジックなんてわかってなくてもいいんです(個人的にはわかったほうがいいと思いますが)。
まず改めてですが、因数分解は展開の逆ですね。
そして別の言い方をすると、展開は分配法則をすることとも言えるので、因数分解は逆分配法則をするとも言えそうです。
ただ厄介なのが、分配法則をする上で外側同士と内側同士の掛け算はのちに足し算をすることになるんですね(今回で言うと8xと3xで緑色の矢印のこと)。
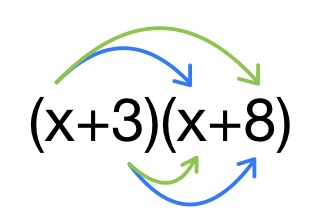
なので、今の話をまとめて逆分配法則をしようとすると、このような図になります。
あらかじめ( )( )を用意しておいて、その中の文字や数字を当てはめようとするのです。
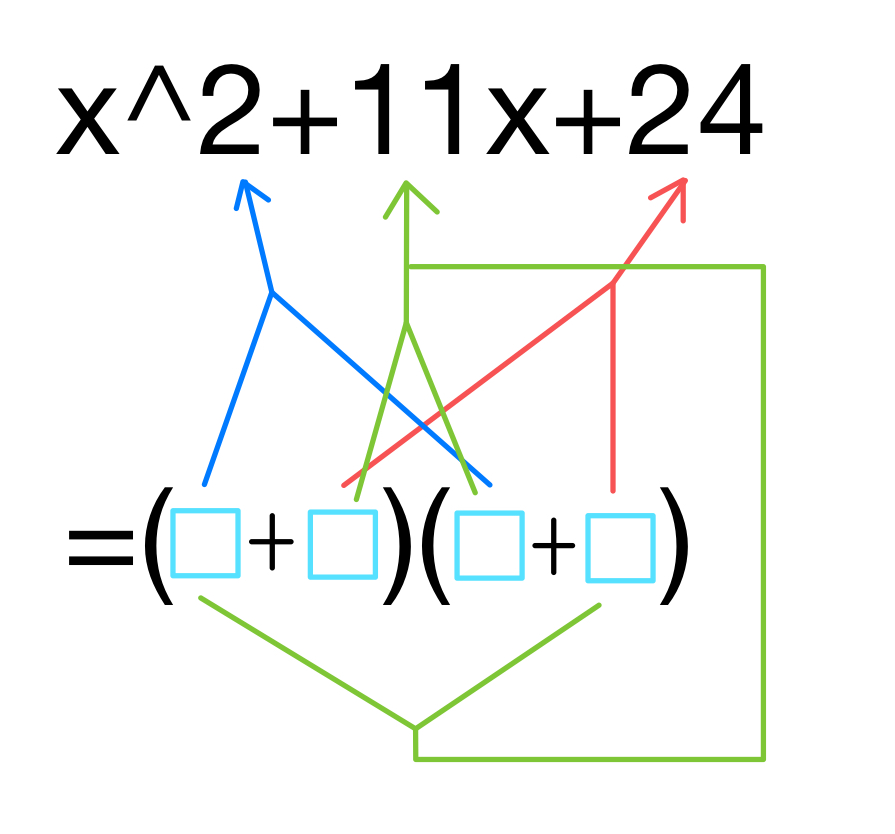
これでやろうとすると、おそらく最初に青矢印と赤矢印を考えて、その後に緑矢印が成立すれば成功でしょう。
もちろんこれで成立します。というか、これが因数分解の根っことなる考え方だと思っています。このやり方が良いなと思ったらこれで因数分解をやっていきましょう!
学校で紹介される公式というのはあくまで結果論に過ぎないのです。
ただ、これは単純に考えにくいと思う方も少なくないと思います。
矢印でさえこんなに汚くなります。そして実際に問題を解くときはこんなに色を使うこともできないでしょう。
そんな時にある頭のいい人がこんなふうに考えたのです。
「( )( )のやつ横じゃなくて、縦に置いたら考えやすいんじゃね?」と。
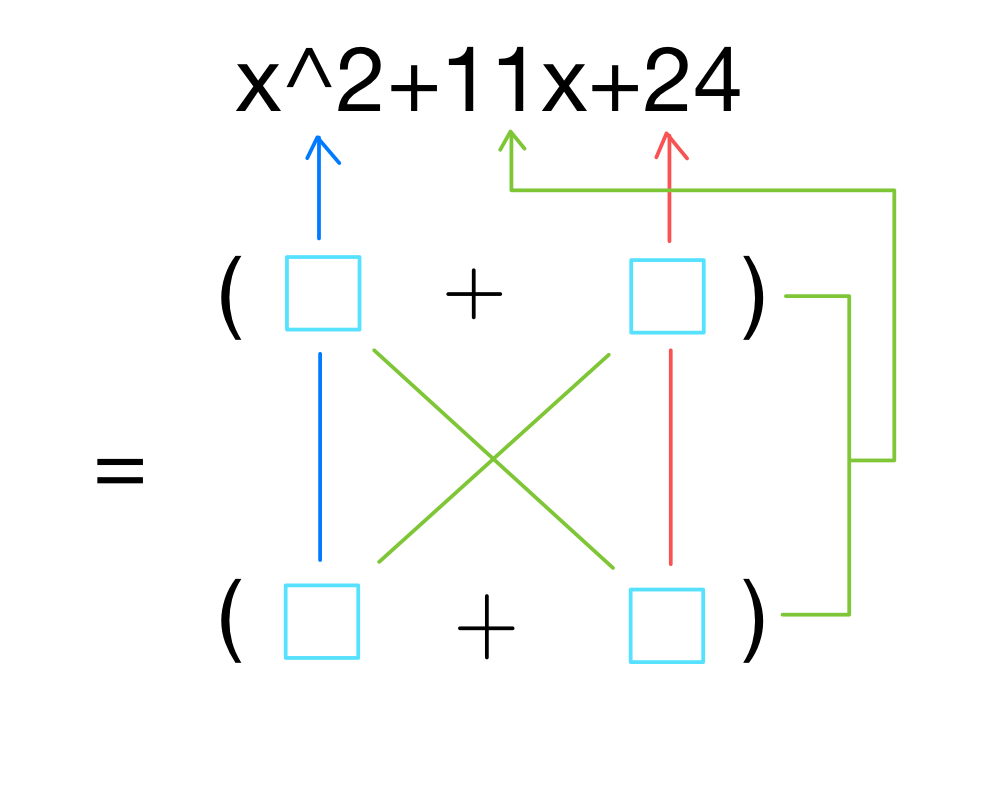
先ほどと同じように逆分配法則を考えたのは同じですが、縦にすることで一気に考えやすくなったのではないでしょうか?
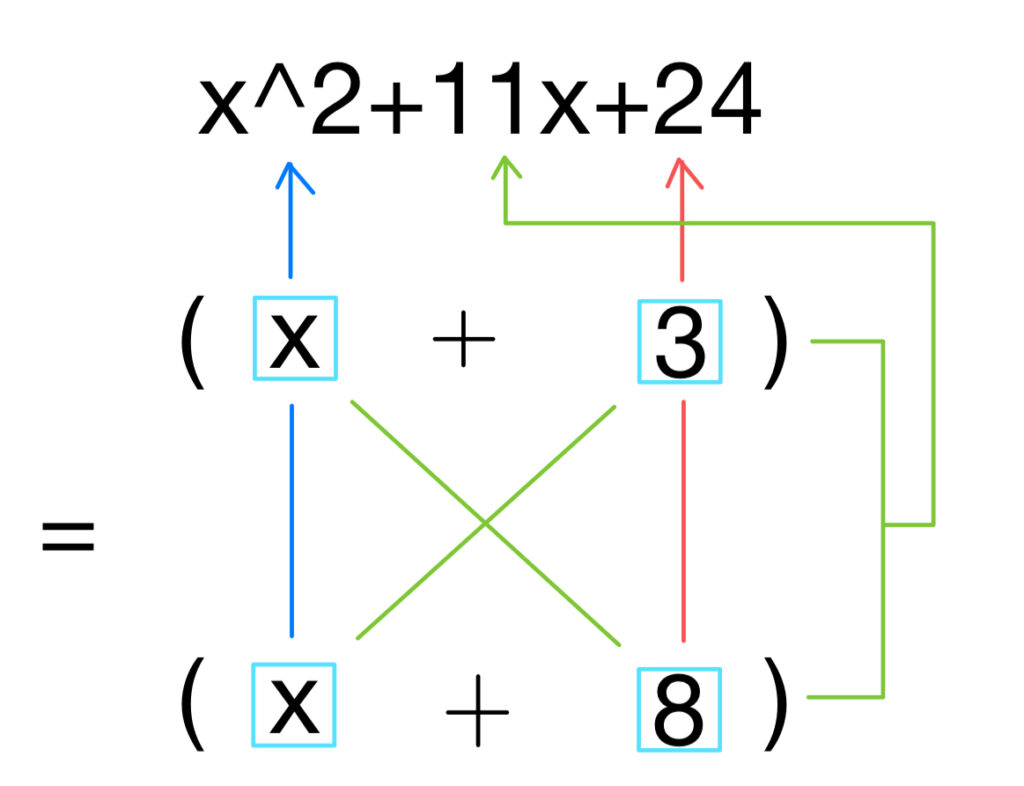
実際に穴埋めをしていきます。
青矢印はかけてx^2になればいいので、左上と左下には両方xが入りそうです。
次に赤矢印ですが、かけて24になる数字を考えます。
色々なパターンが考えられますが、3と8でも成立するので右上と右下に入れてみます。
あとは緑矢印。
ちゃんと掛け算して足すと11xになるので、今回はこれが正解になります。
最初に話した「展開の逆を横ではなく縦に考えているだけだから」という意味が少しでもわかったでしょうか?
展開の逆というのは逆分配法則のことで、縦に考えるというのは( )( )を普通は横にして計算しますが、縦に置くことによって考えやすくしたということです!
結局バッテン方式が成立するのは、ただ( )( )を縦に置いただけだからというふうにも言い換えれそうですね。
因数分解は共通因数とバッテン方式で全部できる
バッテン方式の万能性

バッテン方式で因数分解できるのはわかったんですけど、なぜ4つの公式を網羅できるんですか?

いい質問だね!これから説明していくよ。
上の公式4つのうち一番上を使って、バッテン方式を紹介しました。
本当にした3つをバッテン方式で説明できるのか疑っている方もいると思います。
安心して読んでいってください。本当にうまくいくんです。
まず2,3個目から。
なぜ一気に説明するかというと、この2つは大差ないんです。
上の式でもわかるように、(x+a)^2は(x+a)(x+a)のことなので、それを踏まえてバッテン方式を使ってみます。
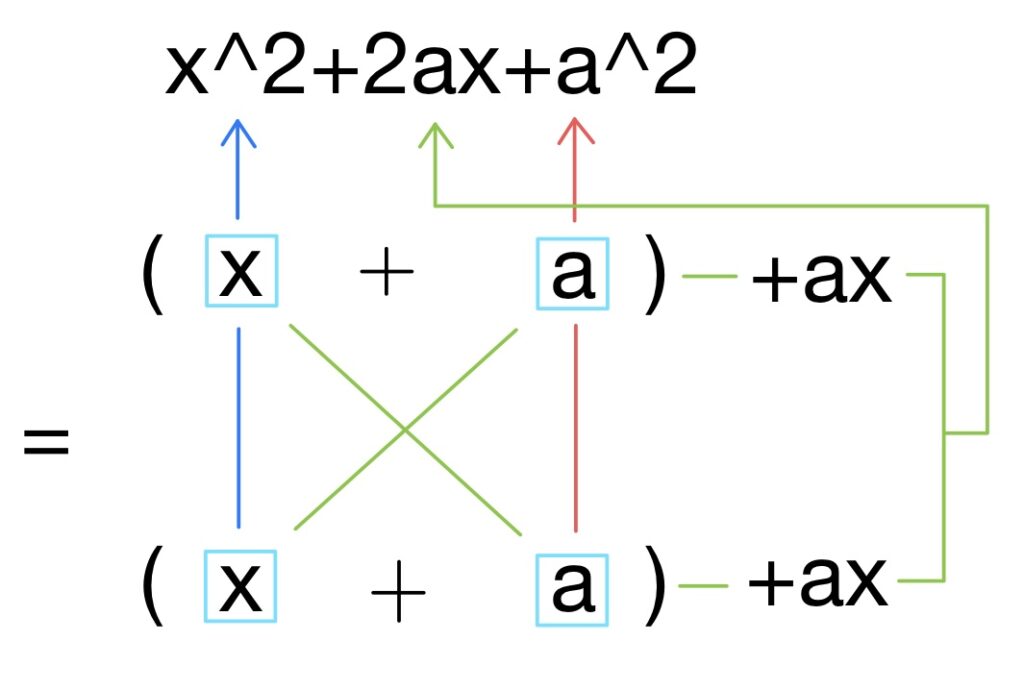
青矢印は先ほどと同じで、赤矢印はかけてa^2になればいいので右上右下ともにaが入りますね。
そして緑矢印を確認してみると上下ともにaxとなり、ふたつを足し算すると2axとなるのでバッテン方式成功となります。
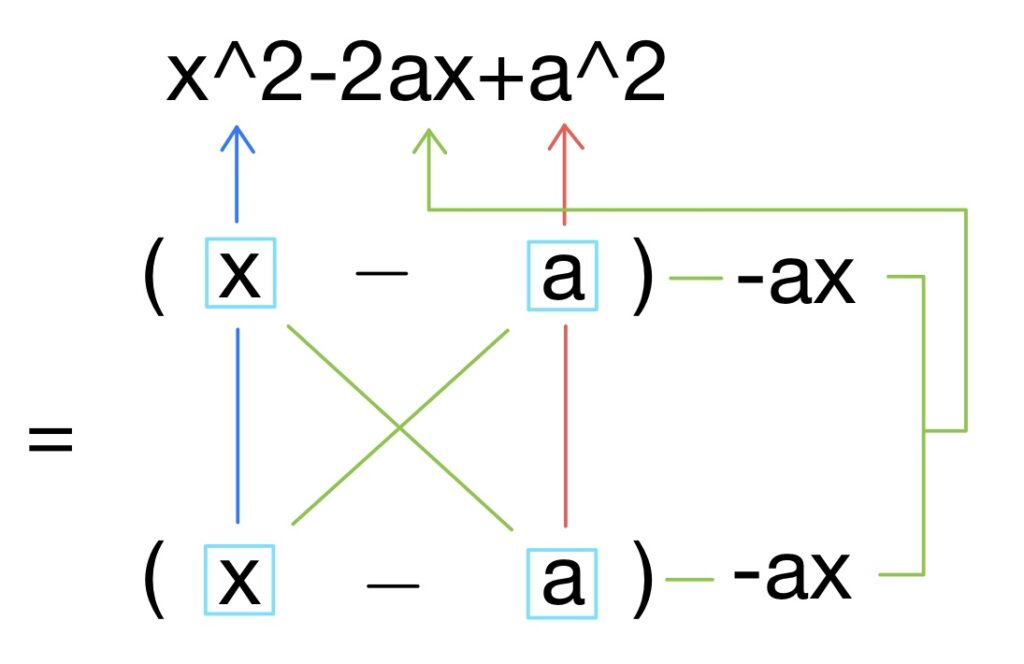
3個目の公式は2個目の公式と全く同じ考え方で、ただ+が-に変わっただけなので、上の図を見ていただければわかっていただけると思います。
そして4個目の公式。
これは今までとちょっと見た目が違いますね。
ぱっと見これはバッテン方式が使え無さそうと思う方がいると思います。
なぜできないと思うのでしょうか?
一体何が違うんでしょうか?
そう、真ん中がないんです!
今までは2乗と2乗の間に何かあったんです。
例えば2axとか、11xとか。
でも今回はないんです。
だからできないじゃないかと思うかもしれませんが、「ない」ということは数字で言うとどう表すでしょうか?
0じゃないですか?
そうなんです!つまり緑矢印のところが0になれば成功となるんです!
それを踏まえてみてみましょう。
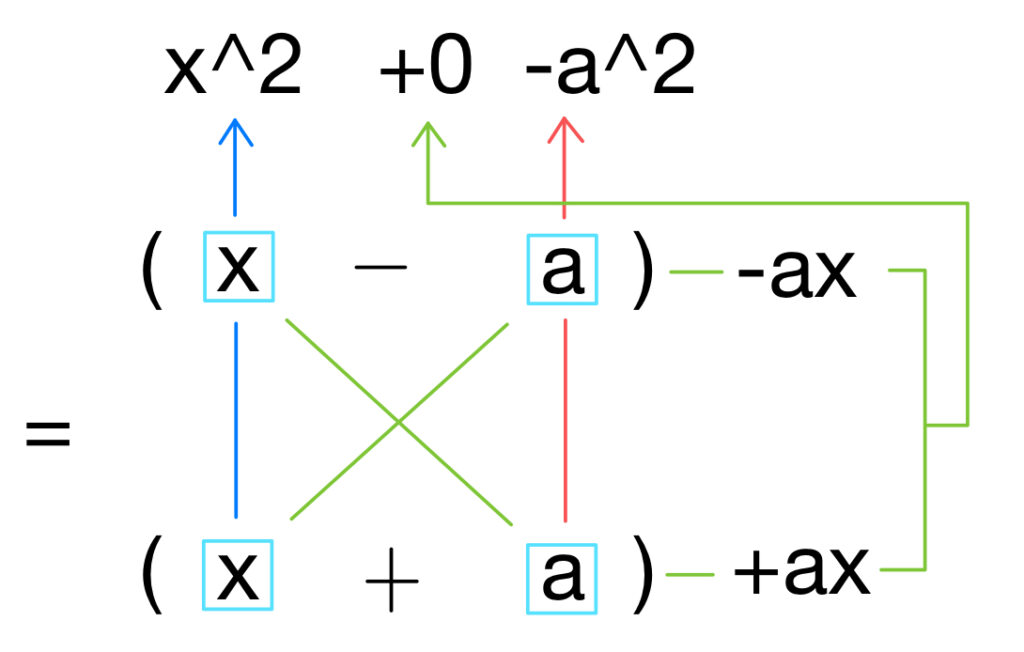
青矢印はいつも通り、そして赤矢印はかけて-a^2になるので、どちらかが+aでどちらかが-aになればうまくいきますね。
そして緑矢印を確認してみましょう。
かけてみると、+axと-axになります。
そしてこれらを足してみましょう。
ちゃんと0になりますね?
なのでこれで因数分解クリアとなります!
いろいろ話しましたが、結局バッテン方式最強じゃんと思っていただけたらそれで十分です。
バッテン方式を使えたら4つの公式を覚えずに済む
まとめ

こんな感じで今日は因数分解について解説したよ

覚えることが大変で嫌いになりそうだったけど、意外としないといけないことは少なくて気持ちが楽になりました。

共通因数とバッテン方式。これだけ覚えて帰ってね。
因数分解は共通因数とバッテン方式で全部できる
バッテン方式を使えたら4つの公式を覚えずに済む
と言うことで、今日は因数分解について記事を書きました。
当時中学生だった自分は理解とかではなく、ただ闇雲に公式を覚えて頑張ってました。
まだ因数分解という単元が嫌いではなかったからギリギリ耐えたものの、苦手な人にとってはとてもしんどい単元だとは思います。
ただその原因はやはり、覚えることが多くて、何の公式や考え方をどう使えばいいかわからなくて、頭の中がメチャクチャになることだと思っています。
今回紹介したように因数分解は共通因数とバッテン方式の2つだけ覚えてくれればよくて、その仕組みも自分なりに説明しました。
一見複雑そうに見える数学ですが、意外と単純だったりもする。
そういうことをしまりす学園では発信していきたいなと思っています!
これからも少しでも多くの数学嫌いの方たちの助けになるような記事を書いていきたいと思うので、よろしくお願いいたします!
別の記事も読んでいただければありがたいです!
改めてここまで読んでくださりありがとうございました!



コメント